Quote:
Originally Posted by sseltser
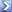
Camron
This is a sweet picture and pretty accurate for our purposes, but there is a slight error that I think you might want to think about.
Consider the area that is inside the ring, but to the "upper left" of the red line. Technically speaking, if the center of the ball happens to drop (straight down or nearly straight down) anywhere inside that area then the ball will bounce toward the center of the basket and have a chance to go in.
Therefore, to get the actual solution for the red line would require this (and I'm not proposing to do this because I've already taken Calc 1 and 2 and don't feel like repeating it):
- The red line would have to be tangent to the curve that is represented by the ring. Therefore, we need en equation of the half circle that is the "upper half" of the ring.
- We probably need to get a function of its derivative.
- Finally we need to find a line that has these three characteristics:
a)passes through the outside point of the backboard (as in the drawing)
b)passes through a point on the ring ( (x,f(x)) where f is the curve of the ring)
C)has the same slope as the instantaneous slope of the curve of the ring that it passes through.
Now that I've done that kind of work for the first time since my sophomore year, if anybody wants to actually figure it out (and find out that the real answer is like 8.6') then they have more free time on their hands than I do.
|
Holy cosine batman!! Juulie and I were wrong.
YOU have too much time on your hands.
